Largest Color Value in a Directed Graph

Leetcode - 1857. Largest Color Value in a Directed Graph

Problem Statement

There is a directed graph of n colored nodes and m edges. The nodes are numbered from 0 to n - 1.

You are given a string colors where colors[i] is a lowercase English letter representing the color of the ith node in this graph (0-indexed). You are also given a 2D array edges where edges[j] = [a_j, b_j] indicates that there is a directed edge from node a_j to node b_j.

A valid path in the graph is a sequence of nodes x1 -> x2 -> x3 -> ... -> xk such that there is a directed edge from x_i to x_i+1 for every 1 <= i < k. The color value of the path is the number of nodes that are colored the most frequently occurring color along that path.

Return the largest color value of any valid path in the given graph, or -1 if the graph contains a cycle.

Example 1:

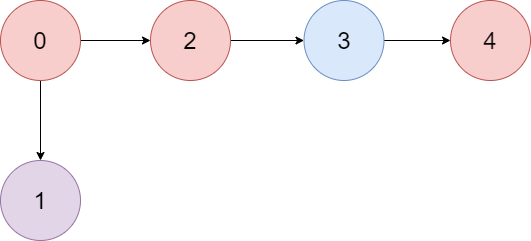
Input: colors = "abaca", edges = [[0,1],[0,2],[2,3],[3,4]]
Output: 3
Explanation: The path 0 -> 2 -> 3 -> 4 contains 3 nodes that are colored "a" (red in the above image).

Example 2:

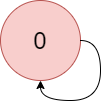
Input: colors = "a", edges = [[0,0]]
Output: -1
Explanation: There is a cycle from 0 to 0.

Constraints:

• n == colors.length
• m == edges.length
• 1 <= n <= 105
• 0 <= m <= 105
• colors consists of lowercase English letters.
• 0 <= aj, bj < n

Solution

class Solution {
public:

    vector<vector<int>> adjList;
    vector<vector<int>> colorValue;
    vector<int> parent;
    string colors;
    int maxColorValue = 1;

    bool hasCycle = false;

    void addEdge(int u, int v) {
        adjList[u].push_back(v);
        parent[v] = u;
    }

    void setup(int n) {
        this->parent = vector<int>(n, -1);
        for (int i = 0; i < n; i++) {
            adjList.push_back(vector<int>());

            vector<int> colors(26, 0);
            int colorIndex = getColorIndex(i);
            colors[colorIndex] = 1;
            colorValue.push_back(colors);
        }
    }

    int getColorIndex(int n) {
        return colors[n] % 97;
    }

    void updateColorValue(int node, int neighbor) {
        int colorIndex = getColorIndex(node);

        for (int i = 0; i < 26; i++) {

            if (i == colorIndex) {
                colorValue[node][i] = max(colorValue[node][i], colorValue[neighbor][i] + 1);
            } else {
                colorValue[node][i] = max(colorValue[node][i], colorValue[neighbor][i]);
            }

            if (colorValue[node][i] > maxColorValue) {
                maxColorValue = colorValue[node][i];
            }
        }
    }

    void dfs(int node, vector<bool>& inStack, vector<bool>& visited) {
        // cout << node << "\n";
        if (inStack[node]) {
            hasCycle = true;
            return;
        }
        inStack[node] = true;

        if (visited[node]) {
            return;
        }

        for (int neighbor: adjList[node]) {
            if (!visited[neighbor]) {
                dfs(neighbor, inStack, visited);
                if (hasCycle) {
                    return;
                }
            }
            updateColorValue(node, neighbor);
        }
        visited[node] = true;

        // for back-tracking
        inStack[node] = false;
    }

    int largestPathValue(string colors, vector<vector<int>>& edges) {
        this->colors = colors;
        int n = colors.size();

        setup(n);

        for (vector<int> edge: edges) {
            addEdge(edge[0], edge[1]);
        }

        vector<bool> visited(n, false);
        vector<bool> inStack(n, false);

        for (int i = 0; i < n; i++) {
            if (parent[i] == i) {
                return -1;
            } else if (!visited[i]) {
                dfs(i, inStack, visited);
                if (hasCycle) {
                    return -1;
                }
            }
        }

        if (hasCycle) {
            return -1;
        }

        return maxColorValue;
    }
};