Design Graph With Shortest Path Calculator

Problem Statement

Leetcode: Design Graph With Shortest Path Calculator

There is a directed weighted graph that consists of n nodes numbered from 0 to n - 1. The edges of the graph are initially represented by the given array edges where edges[i] = [from_i, to_i, edgeCost_i] meaning that there is an edge from from_i to to_i with the cost edgeCosti.

Implement the Graph class:

• Graph(int n, int[][] edges) initializes the object with n nodes and the given edges.
• addEdge(int[] edge) adds an edge to the list of edges where edge = [from, to, edgeCost]. It is guaranteed that there is no edge between the two nodes before adding this one.
• int shortestPath(int node1, int node2) returns the minimum cost of a path from node1 to node2. If no path exists, return -1. The cost of a path is the sum of the costs of the edges in the path.

Example 1:

Input

["Graph", "shortestPath", "shortestPath", "addEdge", "shortestPath"]
[[4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]], [3, 2], [0, 3], [[1, 3, 4]], [0, 3]]
Output
[null, 6, -1, null, 6]

Explanation

Graph g = new Graph(4, [[0, 2, 5], [0, 1, 2], [1, 2, 1], [3, 0, 3]]);
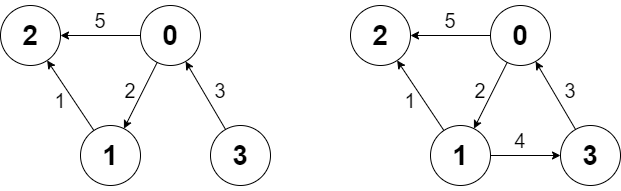
g.shortestPath(3, 2); // return 6. The shortest path from 3 to 2 in the first diagram above is 3 -> 0 -> 1 -> 2 with a total cost of 3 + 2 + 1 = 6.
g.shortestPath(0, 3); // return -1. There is no path from 0 to 3.
g.addEdge([1, 3, 4]); // We add an edge from node 1 to node 3, and we get the second diagram above.
g.shortestPath(0, 3); // return 6. The shortest path from 0 to 3 now is 0 -> 1 -> 3 with a total cost of 2 + 4 = 6.

Solution

typedef priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> distance_queue;

class Graph {
public:

    vector<vector<pair<int, int>>> all_edges;

    Graph(int n, vector<vector<int>>& edges) {
        all_edges = vector<vector<pair<int, int>>>(n);

        for(auto &edge: edges) {
            addEdge(edge);
        }
    }
    
    void addEdge(vector<int> edge) {
        all_edges[edge[0]].push_back({edge[1], edge[2]});
    }

    void visitNode(int node, int baseCost, distance_queue& queue) {
        for(auto &e: all_edges[node]) {
            int distance = baseCost + e.second;
            queue.push({distance, e.first});
        }
    }

    int shortestPath(int node1, int node2) {
        if (node1 == node2) return 0;
        vector<bool> visited(all_edges.size(), false);

        int minDistance = INT_MAX;
        bool pathExists = false;

        distance_queue queue;
        visitNode(node1, 0, queue);
        visited[node1] = true;
        
        while(!queue.empty()) {
            auto current = queue.top();
            queue.pop();

            int node = current.second;
            int distance = current.first;

            if (node == node2) {
                minDistance = min(distance, minDistance);
                pathExists = true;
            } else if (!visited[node]) {
                visitNode(node, distance, queue);
                visited[node] = true;
            }
        }

        return pathExists ? minDistance : -1;
    }
};

/**
 * Your Graph object will be instantiated and called as such:
 * Graph* obj = new Graph(n, edges);
 * obj->addEdge(edge);
 * int param_2 = obj->shortestPath(node1,node2);
 */